Skip to content Skip to sidebar Skip to footer
Home / logaritma

Pembuktian SIfat-sifat Logaritma

Oleh admin Post a Comment
Logaritma adalah kebalikan dari suatu perpangkatan. Jika sebuah perpangkatan ac = b, maka dapat dinyatakan dalam logaritma sebagai:

alog b = c
dengan syarat a > 0 dan a 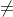 1

maka ac = b jika dan hanya jika alog b = c

C. Pembuktian Sifat-sifat Logaritma
1.^{a}\log a=1
Bukti:
Berdasarkan definisi, ^{a}\log a=1 \Leftrightarrow a^1 = a.
Pernyataan tersebut adalah pernyataan yang selalu bernilai benar untuk setiap nilai a.
Jadi ^{a}\log a=1.
Terbukti.
2. ^{a}\log 1=0
Bukti:
Berdasarkan definisi, ^{a}\log 1=0 \Leftrightarrow a^0 = 1.
Pernyataan tersebut adalah pernyataan yang selalu bernilai benar untuk a \neq 0.
Jadi ^{a}\log 1=0.
Terbukti.
3. ^{a^n} \log b^m= \frac{m}{n} \times ^a \log b
Bukti:
Misalkan  ^{a^n} \log b^m=c.
Berdasarkan definisi,   ^{a^n} \log b^m=c \Leftrightarrow (a^n)^c = b^m.
\\\Leftrightarrow a^{nc} = b^m\\\\\Leftrightarrow b = \sqrt[m]{a^{nc}}\\\\\Leftrightarrow b = a^{\frac{nc}{m}}\\\\\Leftrightarrow \,^{a} \log b = \frac{nc}{m}\\\\ \Leftrightarrow \frac{m}{n}\times ^{a} \log b =c \, \, (\textup{Substitusikan nilai c})
\Leftrightarrow \frac{m}{n} ^{a} \log b = ^{a^n} \log b^m
Jadi  ^{a^n} \log b^m = \frac{m}{n} \times ^a \log b.
Terbukti.
4. \, ^{a^m} \log b^m= \frac{m}{m} \times ^a \log b =\,^a \log b
Bukti:
Pembuktian pada sifat 4 hampir sama dengan pembuktian pada sifat 3, hanya berbeda pada pangkat di basisnya.
Terbukti.
5. ^a \log b = \frac{^m \log b}{^m \log a}
Bukti:
Misalkan  ^a \log b=x
Berdasarkan definisi,  ^a \log b =x \Leftrightarrow a^x = b
\\\Leftrightarrow \,^{m} \log {a^x} = \,^{m} \log b\\\\\Leftrightarrow x \, \times \,^{m} \log {a} = \,^{m} \log b \,\, (\textup{Sifat 3}) \\\\\Leftrightarrow x = \frac{^{m} \log b}{^{m} \log a}\, \, (\textup{Substitusikan nilai x}) \\\\\Leftrightarrow \,^a \log b = \frac{^{m} \log b}{^{m} \log a}
Jadi ^a \log b = \frac{^m \log b}{^m \log a}.
Terbukti.
6. ^a \log b = \frac{1}{^{b} \log a}
Bukti:
Misalkan ^a \log b = x
Dari definisi, ^a \log b = x \Leftrightarrow a^x = b \Leftrightarrow a= b^{\frac{1}{x}}.
\\a = b^{\frac{1}{x}} \\\\\Leftrightarrow \, ^{b} \log a = \frac{1}{x}\\\\\Leftrightarrow x \times ^{b} \log a = 1\\\\\Leftrightarrow x = \frac{1}{^{b} \log a}\\\\\Leftrightarrow \,^{a} \log b = \frac{1}{^{b} \log a}
Jadi ^{a} \log b= \frac{1}{^{b} \log a}.
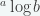
Terbukti.
7. a^{^{a} \log b}=b
Bukti:
Berdasarkan definisi, a^{^{a} \log b}=b \Leftrightarrow ^{a} \log b = ^{a} \log b
Pernyataan tersebut selalu bernilai benar. Terbukti.
8.  ^{a}\log (bc) = ^{a}  \log b + ^{a} \log c
Bukti:
Misalkan ^{a} \log b = x dan ^{a} \log c = y
Berdasarkan definisi:
^{a} \log b = x \Leftrightarrow a^x=b
^{a} \log c = y \Leftrightarrow a^y=c
Dengan mengalikan b dan c diperoleh:
\\b \times c = a^x \times a^y\\\\\Leftrightarrow b \times c=a^{x+y} \,\,(\textup{Sifat eksponen}) \\\\\Leftrightarrow \,^{a} \log (b \times c) = \, ^{a} \log a^{x+y} \,\,(\textup{Sifat 3}) \\\\\Leftrightarrow \,^{a} \log (b \times c)=x+y \,\,(\textup{Substitusikan nilai x dan y}) \\\\\Leftrightarrow ^{a}\log (bc) = ^{a} \log b + ^{a} \log c$
Jadi  ^{a}\log (bc) = ^{a}  \log b + ^{a} \log c.
Terbukti.
9.  ^{a} \log \left ( \frac{b}{c} \right )= ^{a}  \log b - ^{a} \log c
Bukti:
Misalkan ^{a} \log b = x dan ^{a} \log c = y
Berdasarkan definisi:
^{a} \log b = x \Leftrightarrow a^x=b\\ ^{a} \log c = y \Leftrightarrow a^y=c
Dengan membagi b oleh c diperoleh:
\\\left ( \frac{b}{c} \right ) = \left ( \frac{a^x}{a^y} \right )\\\\\Leftrightarrow \left ( \frac{b}{c} \right )=a^{x-y}\,\, (\textup{Sifat eksponen}) \\\\\Leftrightarrow \,^{a} \log \left ( \frac{b}{c} \right ) = \,^{a} \log a^{x-y} (\textup{Sifat 1}) \\\\\Leftrightarrow \,^{a} \log \left ( \frac{b}{c} \right )=x-y (\textup{Substitusikan nilai x dan y}) \\\\\Leftrightarrow ^{a}\log \left ( \frac{b}{c} \right ) = ^{a} \log b - ^{a} \log c
Jadi  ^{a} \log \left ( \frac{b}{c} \right )= ^{a}  \log b - ^{a} \log c.
Terbukti.
10. ^{a} \log b \cdot ^{b} \log c = ^{a} \log c
Bukti:
Sifat ini dapat dibuktikan dengan menggunakan sifat 6 (telah dibuktikan sebelumnya). Untuk mempermudah penulisan, kita gunakan basis 10.
\\ \,^{a} \log b \cdot ^{b} \log c = \left (\frac{\log b}{\log a} \right )\left (\frac{\log c}{\log b} \right ) \\\\ =\left (\frac{\log c}{\log a} \right ) \,\,(\textup{Sifat 5}) \\\\=\,^{a} \log c Jadi ^{a} \log b \cdot ^{b} \log c = ^{a} \log c.
Terbukti.

Post a Comment for "Pembuktian SIfat-sifat Logaritma "